Documentation
The code for GraphSPN uses the libspn library as the SPN library, which is integrated with TensorFlow. Because the libspn was under active development, the code for GraphSPN was compatible to only an earlier version of the libspn, which provided decent performance in terms of memory efficiency and inference speed. There is no current plan from the authors to integrate GraphSPN with new libspn versions, but we welcome contributions.
Using GraphSPN
You will encounter 3 classes: Graph, Template, TemplateSpn, and InstanceSpn. If your use case matches the following assumption:
``you have a dataset of graph-structured data, where the nodes contain information in the form of discrete values, such as the category of a room. These discrete values have been mapped into integers, starting from 0 to the number of possible values.''
then GraphSPN can most likely be useful. The workflow looks like:
- Process your dataset so that each graph can be turned into a
Graphobject. If you only have a single giant graph, break it down into smaller ones so that you can have data for training. - Design a set of sub-graph templates used to partition the graphs. To do so, you need to implement a class that extends the
Templateclass. There are already several templates implemented in thetemplate.pyfile. - Create
NodeTemplateSPNobjects, each for one template in your set of templates. - Train the
NodeTemplateSPNobjects. - For each test graph, instantiate the template SPNs by creating a
NodeTemplateInstanceSpnobject. - Use the
infer_marginalsfunction of the instance SPN object to infer the marginal distribution of latent variables.
A skeleton of code that captures steps 3 to 6 is provided below. You can also refer to the test scripts and reproduce_aaai2018.py for examples.
dataset = setup_dataset()
# Setup template SPNs and train them
templates = [ThreeNodeTemplate, SingletonTemplate, PairTemplate] # could be others
template_spns = [NodeTemplateSpn(template, num_vals=num_vals) for template in templates]
sess = tf.Session()
for i, template in enumerate(templates):
tspn = template_spns[i]
tspn.generate_random_weights()
tspn.init_weights_ops()
tspn.init_learning_ops()
tspn.initialize_weights(sess)
sess.run(tf.global_variables_initializer())
samples = np.array(dataset.create_template_dataset(template),
dtype=np.int32)
train_likelihoods, test_likelihoods \
= tspn.train(sess, samples, shuffle=True, batch_size=batch_size,
likelihood_thres=0.05, num_epochs=num_epochs, dgsm_lh=None,
samples_test=None, dgsm_lh_test=None)
# Setup instance spns
ispn = NodeTemplateInstanceSpn(graph, sess, *[(tspn , tspn.template) for tspn in tspns],
num_partitions=5,
graph_name="graph_name", # if your graph has a name
divisions=8,
super_node_class=SimpleSuperNode, # subclass of SuperNode
super_edge_class=SimpleSuperEdge) # subclass of SuperEdge
assert ispn.root.is_valid()
if Take_Raw_Local_Likelihoods_Inputs:
ispn.expand()
ispn.init_ops(no_mpe=True)
query_nids = [...] # list of node ids you want to query the marginal distribution for
query, likelihoods = setup_test_case(...)
marginals = ispn.infer_marginals(sess, query_nids, query, query_lh=likelihoods)
Regarding SuperNode and SuperEdge, they are useful for partitioning a graph. The pseudocode of the graph partition algorithm is given below:
partition_by_template(G, templates):
G' = G # self
D = {}
for T in templates:
G_super, G_unused = partition(G', T)
G' = G_unused
D[T] = G_super
return D
partition(G, T):
E_super, V_super = {}
E_avail, E_used, V_avail, V_used = prep(G)
while |E_avail| > 0:
e = sample(E_avail)
n1, n2 = e.nodes
if n1 in V_used and n2 in V_used:
if |T.V| > 0:
E_avail.remove(e) # this edge is not useful for matching T
enset = T.match(n1, e, V_used, E_used) # T is edge template. Attempt to match
if |enset| > 0:
E_avail = E_avail / enset.edges
E_used = E_used U enset.edges
V_avail = V_avail / enset.edges
V_used = V_used U enset.edges
v_super = SuperNode(enset) # a supernode with underlying EdgeNodeSet `enset`
make_connections_and_edges(v_super, V_super, E_super)
G_super = Graph(E_super)
V_unused = G.V / V_used
E_unused = G.E / E_used
G_unused = EdgeNodeSet(E_unused, V_unused).to_unused_graph()
return G_super, G_unused
make_connections_and_edges(v_super, V_super, E_super):
enset = v_super.enset
for v in enset.nodes:
: check neighbors. If neighbor belongs to a super node, connect the two.
for e in enset.edges:
: check edges outgoing from both ends. If an edge belong to a super
: node, connect the two.
Below is an example visualization of a graph decomposition attempt:
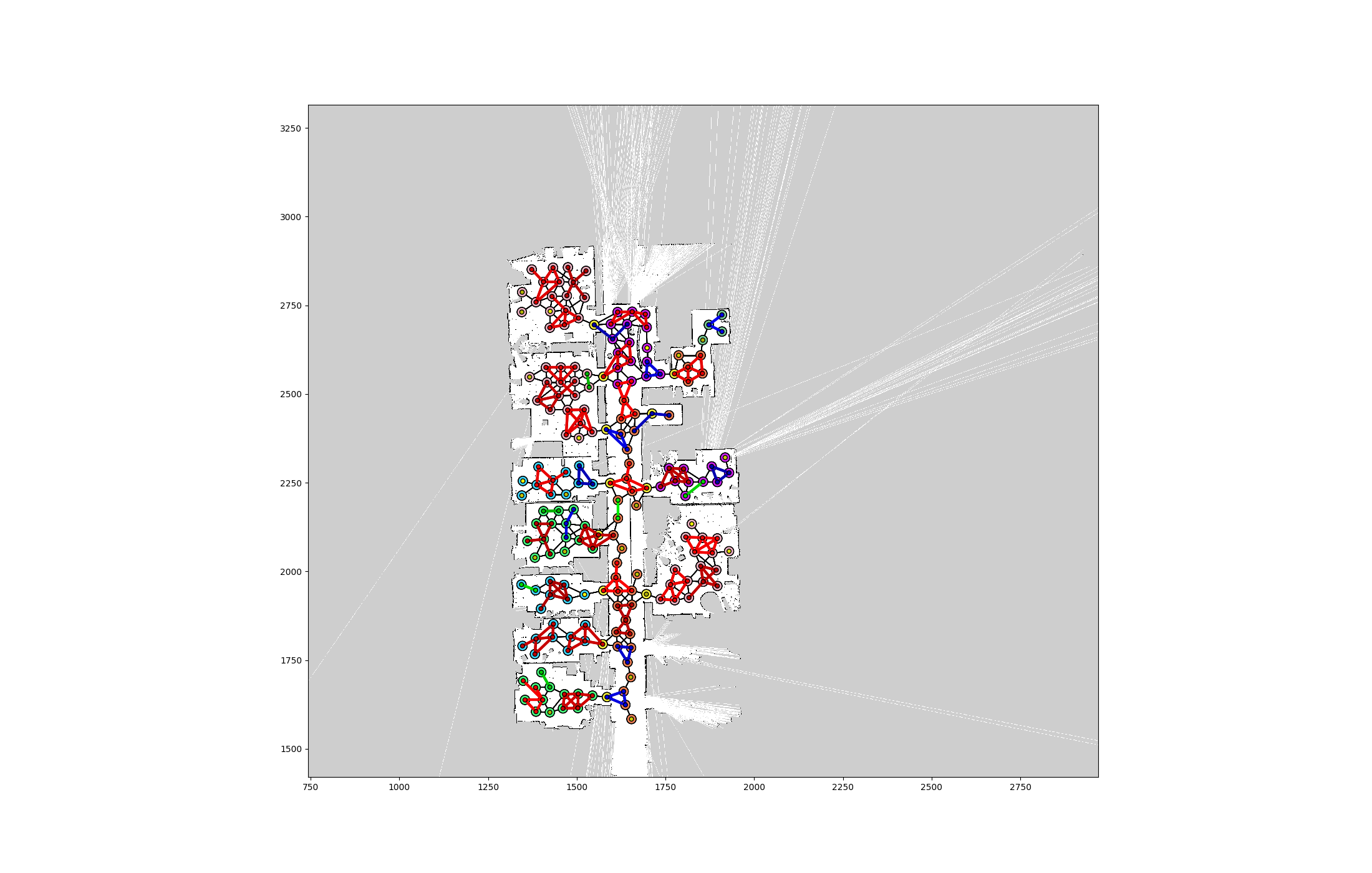
A note on the Graph class. Defined a Graph to be a set of edges, a child class of EdgeNodeSet. An EdgeNodeSet is just a set of nodes and edges, with no rules whatsoever. For an EdgeNodeSet to become a Graph, as implemented in to_graph function, the nodes of edges must also be included in nodes. There is a child class of Graph, the UnusedGraph, which is not intended to be instantiated by the user, and only used as intermediate objects during the partitioning. The unique thing about UnusedGraph is its _partition_setup() function, which only returns nodes and edges that are marked unused. The most important functions in a Graph is the partition_by_templates function.
Memory usage and inference time
To instantiate a GraphSPN for a topological graph of 100 to 150 nodes (each may assume one of 10 semantic labels), with 40 partitions, we observed that the RAM usage (mostly for generating Ops) is usually less than 3 GB. In this setting, the time to infer the marginal distributions of queried variables (i.e. MAP inference) is around 1 second (the first inference attempt takes longer, while all subsequent inference attempts take around 0.5s). A single pass of the network, that is, the marginal inference of P(x,y) takes about 0.19s.
More partitions implies more nodes may be covered by sophisticated templates in different ways, which is helpful for the inference process. Note that, however, at the time of our AAAI'18 paper, a more primitive version libspn was used, which was inefficient in memory usage, limiting the number of partitions we could test with to just 5. With current libspn, a GraphSPN instantiated over 5 partitions of a graph as described above, uses about 0.5 GB RAM, with MAP inference time around 0.4 seconds, and single upward pass time of 0.072s. The inference time scales linearly as the number of nodes in the graph, an expected property of Sum-Product Networks.
(Note that the above numbers are obtained from a workstation with a GTX 1070 GPU, Intel i7 CPU and 16 GB RAM)